THE CREATION OF THE X-STEM LOGIC ALPHABET
Click to Download PDF
Shea Zellweger was born in Chicago in 1925. In general, he calls on the patterns that have repeated in evolutionary notation for the past 3000 years. Three obvious examples tell the story of how we got to where we are in reference to counting (1 2 3), writing (a b c), and singing (doh ray me). All of this is treated as one long and very large laboratory setting, an in vivo laboratory setting that is loaded with one vast expanse of trial and error. This vast expanse then becomes one gigantic seedbed, out of which to engage in the highly specialized act of engineering new notations (sign design and sign engineering). In other words, this approach as method becomes the operating frame within which to extract the best root structure that, in each case, can then be used as the root forms from which to engage in some applied cognitive ergonomics. In particular, he wants to fast forward and repeat the same game for elementary logic (o p b), which are the first three signs in his X‑stem Logic Alphabet (XLA). This is a new notation for the logic of sentences, also called the propositional calculus, also seen as the simplest and the most fundamental layer of symbolic logic.
The creation of the X-stem Logic Alphabet, as it now stands, grew out of a long journey that goes all the way back to the middle of the 20th century. This journey had so many starts and stops that, pulled across many decades, it unfolded in many steps and stages. Certainly suggestive across those decades is what some have called the 10 -year cycle that seems to show in the creative process.
In 1953, following his undergraduate degree at the University of Chicago (1952) and while working as a switchboard operator in a small hotel in Chicago, Zellweger looked upon truth tables only as truth tables when he subjected them to symmetry operations.
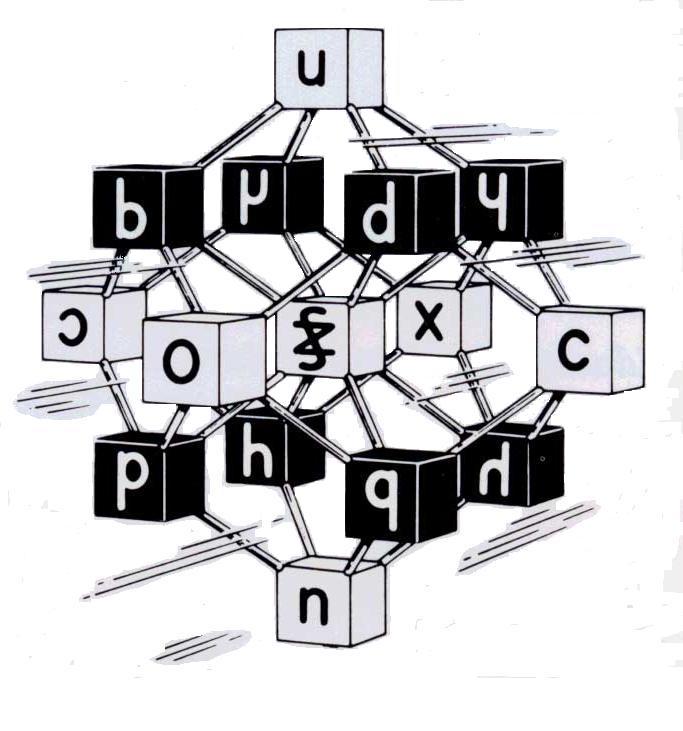
In 1961‑62, while continuing as a graduate student in Experimental Psychology at Temple University in Philadelphia and, out of curiosity, after reading just the right combination of books and articles, Zellweger devised the 16 iconic letter shapes that constitute the X‑stem Logic Alphabet, devised it so that, coded to contain built‑in truth tables, it could be treated as a total system, when it is subjected to symmetry operations. How? The root insight is reminding us that a symmetry demarcated coded square has two axes (A,B), four quadrants (TT,TF,FT,FF), and 16 combinations of those quadrants (FFFF . TFFF . . TFFT . . FTTT . TTTT) --- all of this translated into the 16 4‑fold (stem)(no stem) combinations for the letter shapes (o . d .. s .. h . x).
At this point a strong warning is required. A perfect example here goes back more that a thousand years. This example will be specified later. For now the warning is simple and emphatic. “Do not like Gerbert slip up on a tiny spot!” Also, knowing how to use Roman numerals (I II III) offers little help when one is trying to use Hindu-Arabic numerals (1 2 3). Likewise, knowing all the right moves that are presently in the main stream for standard logic (dot vee horseshoe) (and or if) offers little help and, unfortunately, it also offers many misleading first‑moment thought‑habit assumptions that become blinding barriers, when one is learning how to use the X‑stem Logic Alphabet (o p b).
It takes a fresh start, a willingness to become an active witness, a witness who is open to becoming acquainted with the simplicities and the unexpected economies that have been built into this notation, the same one that can be subjected to symmetry operations.
Especially in 1973‑75, while serving as the Chairman of the Psychology Department at Mount Union College in Alliance, Ohio, Dr Z, as his students called him, constructed a family of simple and carefully designed symmetry models, symmetry models that are hand-held physical objects that facilitate the early exposure, the later learning, and the full use of the X‑stem Logic Alphabet. These symmetry models, even children can manipulate and become familiar with them, are able to participate fully in the tradition of Froebel, Montessori, and Piaget. These models are also devices that led to patents issued in the United States, Canada, and Japan.
In the 1980s and the 1990s, carried in a context that reached across two full-year sabbaticals at the Peirce Edition Project in Indianapolis (IUPUI), including a careful reading of the manuscript called The Simplest Mathematics itself a part of the Minute Logic (1902), especially the many pages surrounding Peirce’s box‑X notation (1902), it has become evident that, historically speaking, box‑X is the primary precursor of X-stem, so much so that X-stem is now seen as a direct continuation of box‑X. This background includes McCulloch’s dot‑X notation (1942), which independently begins with the same path taken by Peirce. These connections suggest that, in contrast to but also in parallel with the Peano‑Whitehead‑Russell notation (PWR) for (and or if), X‑stem could also be called the Peirce‑McCulloch‑Zellweger notation (PMZ). Added to this background, these years led to some publications, this link going to a page located at WWW: logic‑alphabet.net. The eager reader is directed to four of the titles, those that begin with the words “Sign-Creation” (1982b), “Untapped Potential” (1997a), “On a deep correspondence” (1997b), and “Mathelogical” (2003).
Following his retirement in 1993, Dr. Zellweger continues to remain active, still giving voice, pen, and new findings to his notation, the same one that is capable of being subjected to symmetry operations. Note that this comes to no more than the crystallography contained in a few flips, rotations, and counter changes. Yes, the 16 letter shapes in X‑stem are both topological cursives and interrelational icons that are, in the same frame, being treated as symmetry‑group algebraic, 2‑flat tetrahedral, crystallographic molecules, This not only walks head‑on into the 2‑4‑8‑16 subgroups of the 48‑group that describes the high symmetry carbon‑diamond crystal (m3m), also called (Oh), but it also inhabits the (8, 16, 24)‑cell 4D polytopes. His phone number is 1‑330‑823‑1470. His email is zellwes@muc.edu. His mailing address is Mount Union College, Alliance, Ohio 44601. As already mentioned, his Home Page, initiated and maintained by John Puterbaugh, is located as close as a desktop away at WWW: logic‑alphabet.net. Welcome to an open opportunity to add to the mix, all the way from curious beginner to anyone who belongs to a learned discipline and, especially, to anyone who is generating the future.
An excellent place to find out more about the close connection between Peirce's box-X and Dr. Zellweger's X‑stem is to start, among others, with the paper written (in Spanish) by Arnold Oostra. The tables and diagrams alone will make the case. Also of interest are the links to Glenn Clark, Steven H. Cullinane, Louis H. Kauffman, and Bernd Schmeikal. Recently two exhibits have featured the X stem symmetry models. In 2005 Sina Najafi organized Philosophical Toys, held at Apexart, New York City, when Christine Wertheim's Crystal Clear was also published in Cabinet Magazine. In 2007 Christine and Margaret Wertheim, cofounders of The Institute For Figuring, Los Angeles, joined with David Wilson at the Museum of Jurassic Technology, Culver City, California, where the symmetry models continue to be retained and organized in an extremely clarifying display.
In passing, mentioned here as an alert for any sleuth who is inclined to root out errors, the reader should bear in mind that Dr. Zellweger is without formal training, not only in mathematics but also in logic --- not even one course in logic. This has prompted some to call on labels such as “rogue mathematician”, “maverick logician”, also “outsider logician.” As Dr. Zellweger puts it, he sees himself as a melon-sized popcorn ball, with sticky molasses in just the right places, one that has been slowly rolling across the decades. In effect, the creation of the X‑stem Logic Alphabet (XLA) began as an offhand hobby that all too forcefully became an uncompromising monster. In his own words, his notation gradually took on a life of its own as it grew out of “a long run of unschooled and fragmented intuition.”
All of this is telling us that a shape‑value notation called X‑stem is fully prepared to bring some fresh air into geometry. Counting from Peirce and his box‑X notation (1902), we have lost more than a hundred years. The two chief obstacles that plagued the 20th Century are sliding out to sea. First is the Gerbert Barrier from the same Gerbert also known as Pope Sylvester II (999‑1003), who during his travels in Spain did learn to write Hindu-Arabic numerals but, unfortunately, who as long as he lived never did learn how to operate, how to add and multiply with them. This returns to that strong warning about a slip up on a tiny spot. Another Gerbert we do not need: someone who has learned to write the X‑stem letter shapes but, sad to say, someone who has never learned how to operate, how to subject X‑stem to symmetry operations. Notice the four levels of self‑symmetry (across the x‑y axes) within the 16 letter shapes (2 2 4 8) and then one‑to‑one, in perfect correspondence, let the letter shapes line up with the four levels of power that exist in chess pieces all the same color (2 2 4 8). More, a lot more, much easier than this bit of unexpected detail.
Second is Axiomatics In Overdrive which, intended or not, has been pulling the oxygen out of geometry. Disappearing are the days for those who would cling too narrowly to Hilbert and the axiomatization of geometry. Likewise for those who would follow Bourbaki and declare, “Euclid is dead!” Likewise for those, too much notation blind, who would let the narrow‑gauge axiomatics that underlies the Whitehead‑Russell Principia continue to cage, crib, and cabin the propositional calculus. Fortunately, a past is fading and a new era will open doors to the importance of shape‑value notation. In practice, give notation just the right wiff of geometry --- only to discover that the algebra of logic comes up seriously underdeveloped because the algebra of logic does not have enough algebra in it.
Seen against this background and the tides of change, Zellweger claims that X‑stem, when it is subjected to symmetry operations, is now ready to be carried full stride into the 21st Century.