|
|
Simplicity and the Generalization of De Morgan's Laws |
|
|
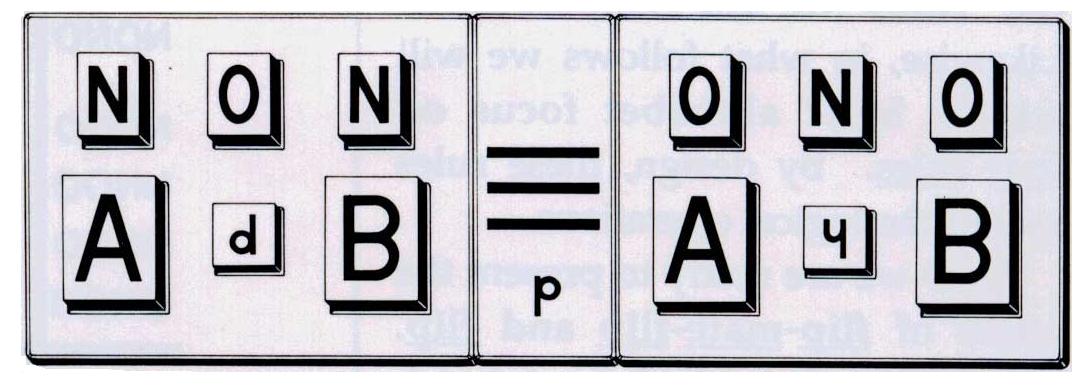
Mirror logic, by analogy from Chomsky, can also be cast as transformational logic. The point here rests on the fact that the symmetry properties contained in square truth tables, as in (2), have been built into the shape-value structure of the LSs, as in (4). Consequently, the sign-making act has been completed in such a way that the formal conditions in the syntax of the LSs have been designed and then specified so that they have been put into a simple and direct isomorphism with the interrelational requirements that exist in the semantics of the truth tables. The model below is made from a set of slot-accepting movable blocks that form and resolve equivalences. The setting on this Equivalence Board shows one of De Morgan's laws. In "dot, vee", (NA dot NB) is equivalent to N(A vee B). In words, it says that (Not-A and Not-B) is equivalent to (A Not-or B). In finger pairs, the two expressions become (Not-A TFFF Not-B) and (A Not-TTTF B). As given in the slotted and carefully framed set of moveable blocks shown below, the mirrors can be used to demonstrate that the equivalence, now fully serving as a miniature equilibrium, is "balanced" (valid). When we rotate on the left (NON) and mate on the right (ONO), both sides become (A p B): in words, (neither A nor B); in finger pairs, (A FFFT B). It so happens that the p-letter in (A p B) is the Nor-gate, sometimes expressed as the down dagger (A | B) and also known as the (p)eirce connective.
|
|
|
|
|
Resolving equivalences when they are written in the Logic Alphabet repeats what is done to resolve identities in trigonometry. Change either side into the other side, or change both sides into the same third expression. De Morgan's laws, both of them, come to no more than (i) rotate the LS on the left, (ii) mate the LS on the right, and (iii) thereby obtain the same third expression, that is, the same LS on both sides. In effect, serving as a nice example of cognitive ergonomics at its best, and again calling attention to a fundamental triple isomorphism, the self-same transformations for the symmetry operations line up with the mental operations in such a way that both line up with the logic operations. This arrangement makes it easy to introduce a generalization of De Morgan's laws. As an exercise, find another pair of LSs, and more challenging, all possible pairs, that can be subjected to the same pattern of equivalence-determined symmetry mirrors, namely, (NON) on the left and (ONO) on the right, as these two negation triplets now appear in the top row of the Equivalence Board above. |
|
|
|
|