|
|
Flipstick and Clock-Compass
|
||
|
|
|||
|
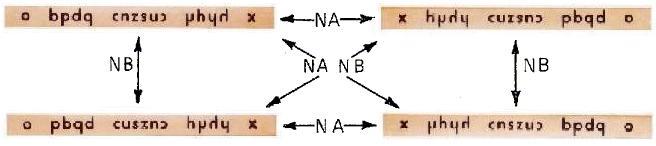
A standard row of LSs (lower left above) occupies the home-row of a model that is called a Flipstick. It repeats the first row of Table I, and it has another set of LSs on its backside, in see-through placement. R1 flips it to the right, R3 flips it upward, and (R1, R3) rotates it around to the upper right. Note especially that a flipstick, taken as a single unit, is acting on all of the LSs, on all of them at the same time and on all of them in the same way. Again, all of this releases the transformational power contained in a small number of symmetry rules (f-m-f and f). |
|||
|
|
|
|
|
|
|
The diamond-shaped 4-by-4 pattern on the left is called a Clock-Compass. This view of the logic alphabet has 12 LSs around the outside, at the positions of a clock, and 4 LSs in the middle, at the directions of a compass. The eight odd-stemmed LSs (- 4 - 4 -) are tall and black. The eight even-stemmed LSs (1 - 6 - 1) are squat and white. The four LSs that have been added at the corners repeat the one-stemmed cursives. The changes in these positions are isomorphic to what happens when combinations of (R1, R3) act on the subset (p, b, q, d). In other words, the symmetry operations for the combinations of (R1, R3), also called the Klein 4-group for (N – N -), are acting on this 4-set of LSs. |
||
|
|||