Logic Bug and Logical Garnet
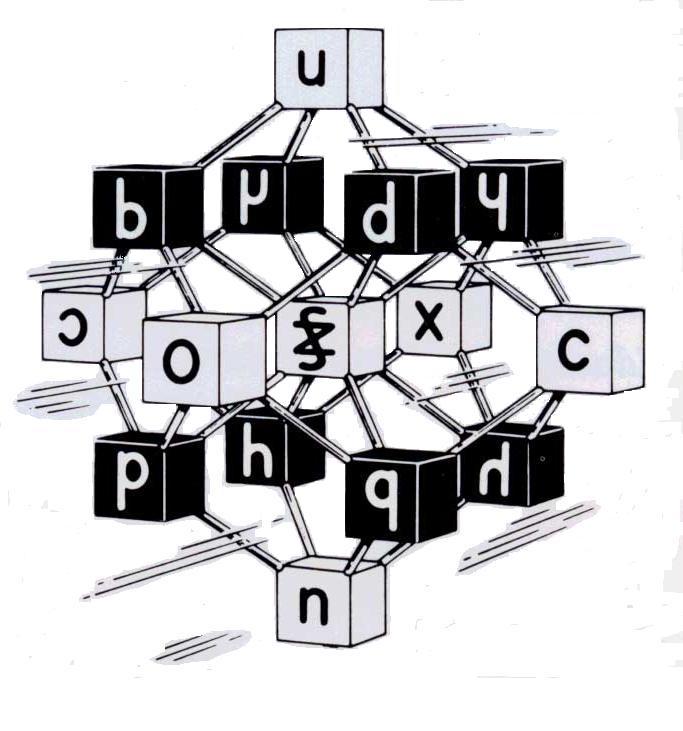
The composite display on the right is called a Logic Bug. It is a 2-D arrangement of the 16 LSs. It comes from pushing nonstop against a head-on view of the Logical Garnet (below) until it becomes as flat as a pancake. Like the 1-D arrangement on the Flipstick, it can also be subjected to the identity-flip-flip-rotate symmetry changes. Right here the logic bug is telling us that a symmetry operation that performs a logical calculation has become something very special and very powerful. Not only is it mirror driven. It is also making a symmetry calculation. "And that," said the Logic Bug, fully in the tradition of Froedel, Montessori and Piaget, "is precisely what I have been designed to do." Now we can make a statement for R2. Look symmetrically across the center in these models to find the mate of any LS. The 16 LSs in the Logical Garnet (below) have been placed at the vertices of a special polyhedron, one that takes the shape of a rhombic dodecahedron. In a league all by itself, this model is called a shadow rhombic dodecahedron. In other words, the 16 vertices of a 4-cube have been shadowed, or projected, into 3-D. Consequently, this model absorbs the flip-mate-flip and flip symmetry properties that have been built into the LSs and that now appear in Table I. These are the same symmetry properties that isomorphically line up with the networks of interrelations that inhabit the 16 binary connectives. In other words, and this is a significant point, the same symmetry calculations are activated when the symmetry-driven LSs isomorphically circulate throughout the networks of interrelations.
previous page | next page