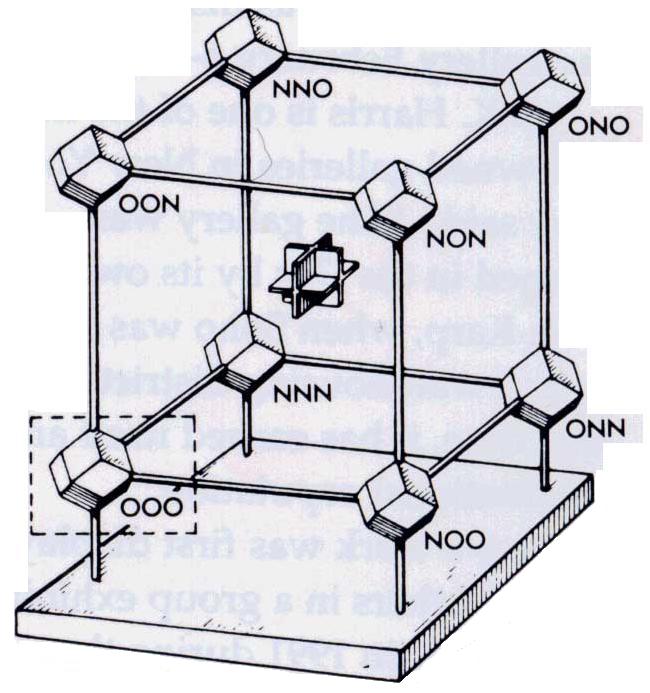
An Eight-Cell of Logical Garnets
What happens when a Logical Garnet becomes a basic unit that is used to display more complex structure? The three mirrors (for flip-mate-flip) could be put at right angles to each other. Another way to set up a vector space is to let R2 go through the center, a center of inversion, which forces duality (NNN) to become the 3rd dimension (front to back). This has been done for the 8-cell of Logical Garnets shown below. This model is for the 128 cells in the top half of Table I. Taken from the first row of Table I, the identity garnet (OOO) has been placed in the dash-lined rectangle. The other seven garnets are now in perfect alignment with the other seven rows in the top half of Table I. Also seen as the product of (N, N, N, -) times (A * B), the eight 16-sets of LSs in this model come from taking the product of two Boolean lattices, in this case from the product of the operations (1 3 3 1) times the connectals (1 4 6 4 1).
We want no part of misplaced axiomatics. Along with emphasizing the importance of notational primitives, we do not try to isolate a small number of axiomatic primitives (such as "and", "nand", "nor") that will best cut into the abstract structure that contains the product of the Boolean lattices. Note that R4 adds a diagonal mirror to the symmetry operations. This introduces the bottom half of Table I, which will then include exactly all of the 256 cells (16 by 16) in the new multiplication table.
The well-ordered complexity in Table I deserves to be made more explicit. This table is obtained from (1 4 6 4 1) times (1 4 6 4 1). The product of these two Boolean lattices can also be seen as what happens when a symmetry-based 16-set obtained from the four combinatory logical operations along the left side (N, N, N, C) is acting on a custom-selected symmetry-designed 16-set of notational primitives, namely, the special set of binary connectals across the top (A * B), also called the logic alphabet. In effect, this line of system building, starting with a 16-set of notational primitives, is a ready-made introduction to Clifford algebras.
previous page | next page