Mirror Logic and Networks of Abstract Graphs

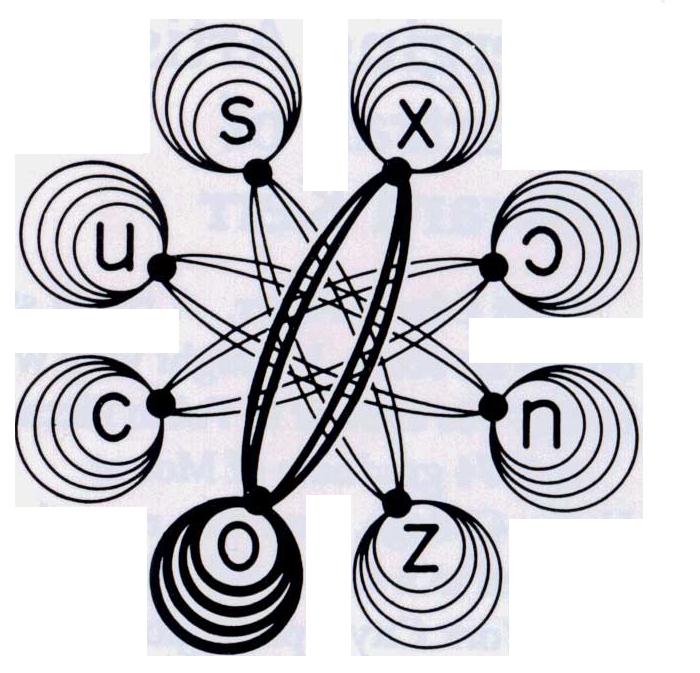
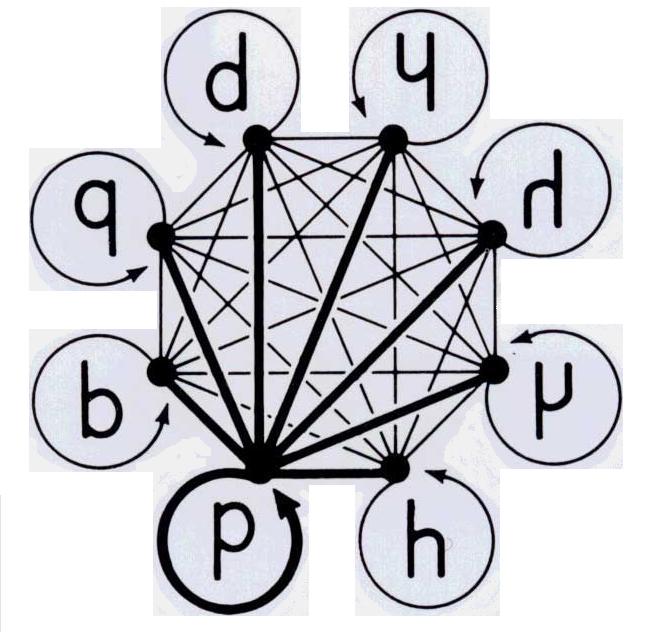
The figures on this page go with the top half of Table I. In another context, the network on the right also appears in Ramon Lull (1235? - 1315). The network on the right is for the odd-stemmed LSs (- 4 - 4 -); the network below is for the even-stemmed LSs (1 - 6 - 1). The eight LSs on the right occupy the vertices of a cube and the eight below are at the vertices of an octahedron (two at the cocenter). These two geometric solids are seen as 3-D objects that interpenetrate in the Logical Garnet. It follows that the Logical Garnet becomes a key player because it is fully able to let 3-D mirrors act on a 3-D arrangement of a 4-D count of the 2-D signs, all of them serving as a special 16-set of connectals (not numerals). The same set of stem shapes appears in the dot squares on the Clock Compass. These configurations happen to display the logic alphabet in a particular way, but, once we know what to do, there are many ways to embody the same primary structure in a large family of hand-held models.

A symmetry approach to the 16 binary connectals should leave no doubt that we have a very unusual tiger by the tail. Another insight comes from realizing that Arabic numerals happen to be an abacus that has been lifted to the mental level. Likewise, the LSs are small Venn-Carroll-Cartesian diagrams raised to the mental level. Ordinary Venn diagrams are cement-heavy stuck to the page. So are the lines and squares that frame an ordinary crossword puzzle. In contrast, using the logic alphabet is using a shape alphabet in a spatial logic. It is even more fluid and flexible than playing a game of ordinary scrabble. When the LSs operate at the mental level, the logical form under consideration becomes the scrabble frame. Then the LSs become a primitive set of Venn-Carroll-Cartesian fragments. Then the LSs are pushed around in a thought world open to variations in the logical structure. This repeats another way that Arabic numerals are superior to Roman numerals. The act of writing the LSs has become an integral part of making symmetry calculations, thereby introducing another way to engage in computational writing.

previous page | next page